Binary Subtractor
A Binary Subtractor is a digital circuit that performs the arithmetic binary subtraction between two numbers with respect to the logic operations and laws of Boolean Algebra.
The subtractors are used in combinational circuit design and the Arithmetic Logic Unit (ALU) of the processor to calculate multiple addresses. Subtractor circuits reduce sound distortion in amplifiers and the power of radio signals.
There are two types of Subtractor circuits-
- Half Subtractors
- Full Subtractors
Half Subtractors
Half Subtractors are a type of digital circuit that calculates the arithmetic binary subtraction between two single-bit numbers. It is a circuit with two inputs and two outputs.
For two single-bit binary numbers A and B, a half subtractor produces two outputs.
- A is known as the Minuend Bit
- B is called Subtrahend Bit.
- Output D is the difference between the two input bits (A-B).
- Output P is the previous borrow between the two input bits (A-B).
The previous borrow is for the most significant bit (MSB).
Operation and Truth Table for Half Subtractor
Operation:
Case 1: A = 0, B = 0;
According to Binary subtraction, the difference of these numbers is 0 with no previous borrow.
0
– 0
one by one
0
one by one
Hence, D= 0, P= 0
Case 2: A= 0, B= 1;
According to Binary subtraction, the difference between these two numbers is 1 with a previous borrow of 1.
0
– 1
→1 (Previous Borrow)
one by one
1
one by one
Hence, D= 1, P= 1
Case 3: A= 1, B= 0;
As per Binary subtraction, the difference between these two numbers is 1 with no previous borrow.
1
– 0
one by one
1
one by one
Hence, D= 1, P= 0
Case 4: A= 1, B= 1;
According to Binary subtraction, the difference between these two numbers is 1 with no previous borrow.
1
– 1
one by one
0
one by one
Hence, D= 0, P= 0
Truth Table:
| A | B | Difference (S) | Previous Borrow (P) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Designing K-Map for Half Subtractor
By the Truth Table, We can design a Karnaugh Map or K-Map for Half Subtractor to obtain a Boolean Expression.
We can design a Karnaugh Map or K-Map for Half Subtractor to obtain a Boolean Expression.
Karnaugh Map for Difference of Half Subtractor
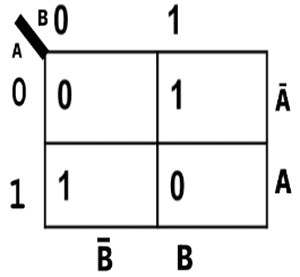
By solving this,
D= A’B + AB’
![]()
Karnaugh Map for Previous Borrow of Half Subtractor
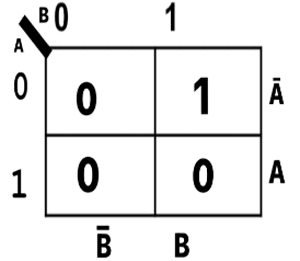
By looking at the K-map, We can conclude, we can conclude;
P= A’•B
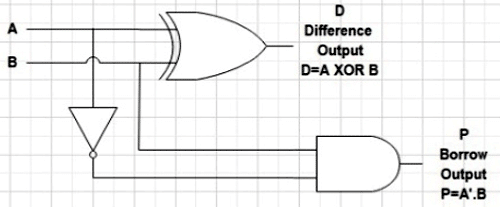
This Boolean expression helps us to design a half subtractor with an XOR Gate and AND gate.
The operation of the Half Subtractor is limited because it can only subtract two-bit binary digits. It does not account for the borrow of the lower significant stage.
This inability of the circuit puts a limitation on its use. Half Subtractors were used in early microprocessors and basic digital circuits.
Designing Half Subtractor using Basic Logic Gates followed by NAND Gate
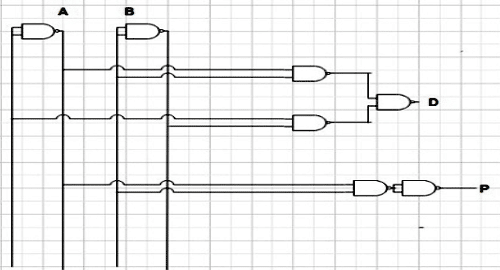
As,
D= A’B + AB’
Taking double complement
![]()
According to d-Morgan’s law,
![]()
Similarly, for the previous borrow circuit,
P= A’•B
Taking double complement
![]()
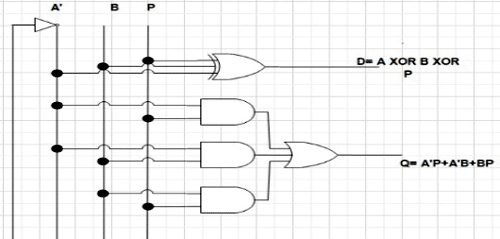
Full Subtractor
A full Subtractor is a digital circuit that performs the subtraction of three single-digit binary numbers. This is a three-input and two-output digital circuit.

For three single-bit binary numbers A, B, and P, the full subtractor circuit generates two single-bit binary outputs D (Difference), and Q (Borrow Output).
- A is the Minuend.
- B is the Subtrahend.
- P is the Previous Borrow Bit.
- D is the Difference between A, B, and P.
- Q is the Borrow Output.
A full Subtractor was made to overcome the limitations of a Half Subtractor.
Full Subtractors are used in-
- Performing Arithmetical functions like subtraction in ALU of Microprocessors.
- Electronic Calculators
- Digital Devices
- Computing Address Tables in ALU.
- DSP and networking-based systems.
Operation and Truth Table for Full Subtractor
Operation:
Case 1: A= 0, B= 0, and P= 0;
The difference of the three binary numbers 0, 0, and 0 produces a difference of 0 and generates no borrow output.
0
-0
-0
one by one
0
one by one
Hence, D= 0, Q= 0
Case 2: A= 0, B= 0, and P= 1;
The difference of the three binary numbers 0, 0, and 1 produces a difference of 1 and generates a borrow output bit.
0
-0
-1
→1
one by one
1
one by one
Hence, D= 1, Q= 1
Case 3: A= 0, B= 1, and P= 0;
The difference of the three binary numbers 0, 1, and 0 produces a difference of 1 and generates a borrow output bit.
0
-1
→1
-0
one by one
1
one by one
Hence, D= 1, Q= 0
Case 4: A= 0, B= 1, and P= 1;
The difference of the three binary numbers 0, 1, and 1 produces a difference of 0 and generates a borrow output bit.
0
-1
→1
-1
one by one
0
one by one
Hence, D= 0, Q= 1
Case 5: A= 1, B= 0, and P= 0;
The difference of the three binary numbers 1, 0, and 0 produces a difference of 1 and generates no borrow output.
1
-0
-0
one by one
0
one by one
Hence, D= 1, Q= 0
Case 6: A= 1, B= 0, and P= 1;
The difference of the three binary numbers 1, 0, and 1 produces a difference of 0 and generates no borrow output.
1
-0
-1
one by one
0
one by one
Hence, D= 0, Q= 0
Case 7: A= 1, B= 1, and P= 0;
The difference between the three binary numbers 1, 1, and 0 produces a difference of 0 and generates no borrow output.
1
-0
-0
one by one
0
one by one
Hence, D= 0, Q= 0
Case 8: A= 1, B= 1, and P= 1;
The difference between the three binary numbers 1, 1, and 1 produces a difference of 1 and generates a borrow output bit.
The difference between A=1 and B=1 is 0. P=1 gets subtracted from this 0 to produce an output of 1 by generating a borrowed output bit.
1
-1
-1
→1
one by one
1
one by one
Hence, D= 1, Q= 1
Truth Table:
| A | B | P | Difference (D) D= A-B-P | Borrow Output (Q) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Designing K-Map for Full Subtractor
By the Truth Table, We can design a Karnaugh Map or K-Map for Full Subtractor to obtain a Boolean Expression.
Karnaugh Map for Difference of Full Subtractor:
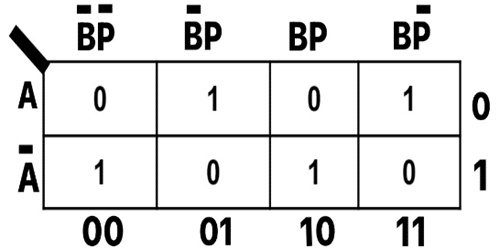
By Solving this,
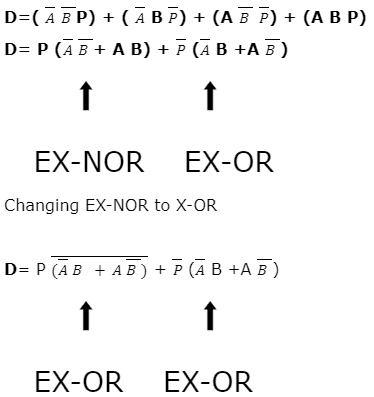
The terms ![]() form a complement of each other, and the whole equation becomes an EX-OR operation;
form a complement of each other, and the whole equation becomes an EX-OR operation;
![]()
Simplifying further,
![]()
Karnaugh Map for Borrow Output of Full Subtractor:
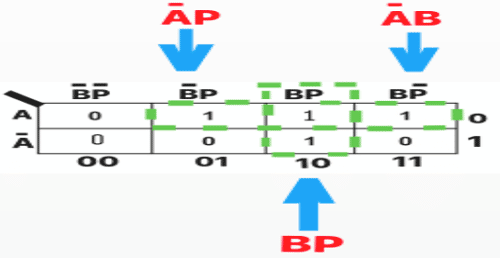
The equation becomes,
![]()
This is the end of the article…..
If you have any doubts, please feel free to ask in the comments below or you can use our Forum to start the discussion with the community of experts.
More details about Subtractor if interested.

